该公告已过公示时间,对该公告内容进行下架处理,给您带来的不便敬请谅解。
【试题练习】
一个半径 300米的圆形湖泊中有一个半径100米的圆形人工岛,该人工岛的中心在湖泊中心的正西方150米处(如图)。甲从湖正北的A点开船出发,绕行人工岛西侧到达正南的B点。问如保持最短路线行驶,其行驶多少米后到达人工岛的岸边?

A.
B.300
C.
D.
正确答案:C
【解析】第一步,本题考查几何问题,属于平面几何类。
第二步,

如图,若保持最短距离行驶,则走的最短路径为直线AE-弧EF-直线FB,从A点出发到E点即达到人工岛的岸边,即求AE的长。连接CD,过A点作圆D的切线,交圆D于E点,连接ED、AD、AC,由题意可得,CD=150米,ED=100米,AC=300米,根据勾股定理得,AD=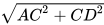 =
=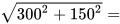 150
150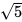 米。
米。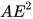 =
=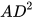 -
-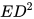 =
=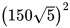 -
-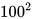 =50
=50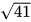 米。
米。
因此,选择C选项。

(编辑:luxianyue)