该公告已过公示时间,对该公告内容进行下架处理,给您带来的不便敬请谅解。
【试题练习】
甲、乙、丙、丁四个队参加五项比赛,每项第一名得3分,第二名得2分,第三名得1分,第四名不得分,已知甲队获得了3次第一名,乙队获得了3次第二名,那么得分最少的队的分数不可能超过( )分。
A.5
B.6
C.7
D.8
正确答案:C
【解析】第一步,本题考查最值问题,属于数列构造类。
第二步,5场比赛总分为(3+2+1+0)×5=30(分),平均每队得分为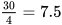 (分)。
(分)。
第三步,甲队获得了3次第一名,甲最少得3×3=9(分),高于平均得分,不可能为得分最少的队;乙队获得了3次第二名,乙最少得2×3=6(分),低于平均得分,有可能为得分最少的队。
第四步,“不可能超过”意味着得分最少的队得分应尽量高,总分一定,则其他队伍得分应尽可能低。乙、丙、丁均有可能为得分最少的队伍,设其得分均为x,构造9、x、x、x的数列,则9+x+x+x=30,解得x=7分。
因此,选择C选项。

(编辑:zhangfangmin)