ёГ№«ёжТС№э№«КҫКұјдЈ¬¶ФёГ№«ёжДЪИЭҪшРРПВјЬҙҰАнЈ¬ёшДъҙшАҙөДІ»ұгҫҙЗлБВҪвЎЈ
ЎҫКФМвБ·П°Ўҝ
ҙУ1Ўў2Ўў3Ўў4Ўў5ЦРЛж»ъійИЎ3ёцКэЈ¬ОКХв3ёцКэЦ®әНЦБЙЩДЬұ»ЖдЦРТ»ёцКэХыіэөДёЕВККЗ¶аЙЩЈҝ
A.10%
B.30%
C.60%
D.90%
ХэИ·ҙр°ёЈәD
ЎҫҪвОцЎҝөЪТ»ІҪЈ¬ұҫМвҝјІйёЕВКОКМвЈ¬КфУЪ·ЦАа·ЦІҪРНЎЈ
өЪ¶юІҪЈ¬ҙУ5ёцКэЧЦЦРійИЎ3ёцКэЈ¬№ІУР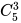 ЈҪ10ЧйЈ¬ВъЧгМхјюУР3ЦЦЗйҝцЈә
ЈҪ10ЧйЈ¬ВъЧгМхјюУР3ЦЦЗйҝцЈә
ЈЁ1Ј©ійіцөДИэёцКэЧЦЦРЦ»ТӘУР1јҙВъЧгЈ¬УР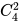 ЈҪ6ЈЁЧйЈ©ЎЈ
ЈҪ6ЈЁЧйЈ©ЎЈ
ЈЁ2Ј©ійіцКэЧЦЦРУР2ЗТГ»УР1Ј¬№ІУРЈЁ2Ўў3Ўў4Ј©Ј¬ЈЁ2Ўў3Ўў5Ј©Ј¬ЈЁ2Ўў4Ўў5Ј©3ЧйЈ¬ЖдЦРЈЁ2Ўў3Ўў4Ј©Ц®әНОӘ2Ј«3Ј«4ЈҪ9Ј¬ҝЙұ»3ХыіэЈ»ЈЁ2Ўў3Ўў5Ј©Ц®әНОӘ2Ј«3Ј«5ЈҪ10Ј¬ҝЙұ»2әН5ХыіэЈ»ЈЁ2Ўў4Ўў5Ј©Ц®әНОӘ11Ј¬І»ДЬұ»ЖдЦРИОТвТ»ёцКэЧЦХыіэЈ¬№КУР2ЧйЎЈ
ЈЁ3Ј©ійіцКэЧЦЦРГ»УР1әН2өДЗйҝцЈ¬Ц»УРЈЁ3Ўў4Ўў5Ј©Ј¬ЖдәНОӘ3Ј«4Ј«5ЈҪ12Ј¬ҝЙұ»3ХыіэЈ¬УР1ЧйЎЈ
өЪИэІҪЈ¬№ІУР6Ј«2Ј«1ЈҪ9ЈЁЧйЈ©ВъЧгМхјюЈ¬ёЕВКОӘ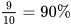 ЎЈ
ЎЈ
ТтҙЛЈ¬СЎФсDСЎПоЎЈ

ЈЁұајӯЈәyaoxingkunЈ©

