该公告已过公示时间,对该公告内容进行下架处理,给您带来的不便敬请谅解。
【试题练习】
有两箱数量相同的文件需要整理。小张单独整理好一箱文件要用4.5小时,小钱要用9小时,小周要用3小时。小周和小张一起整理第一箱文件,小钱同时开始整理第二箱文件。一段时间后,小周又转去和小钱一起整理第二箱文件,最后两箱文件同时整理完毕。则小周和小张、小钱一起整理文件的时间分别是:
A.1小时,2小时
B.1.5小时,1.5小时
C.2小时,1小时
D.1.2小时,1.8小时
正确答案:A
【解析】解法一:
第一步,本题考查工程问题,属于时间类。
第二步,赋一箱文件的工作量为9(4.5、9和3的最小公倍数),则小张、小钱、小周的工作效率分别为2、1、3。根据同时开始、同时结束,可得整理两箱文件的总时间为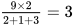 (小时)。
(小时)。
第三步,对于第一箱文件,工作量共为9,小张3小时的工作量为2×3=6,则小周工作量为9-6=3,则小周和小张一起整理的工作量即为3,时间为 =
=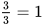 (小时),则小周和小钱一起整理的时间为3-1=2(小时)。
(小时),则小周和小钱一起整理的时间为3-1=2(小时)。
因此,选择A选项。
解法二:
第一步,本题考查工程问题,属于时间类。
第二步,设小周和小张一起整理的时间为t小时,则小周和小钱一起整理的时间为3-t。由工作量相等得,2×3+3t=1×3+3×(3-t),解得t=1。
因此,选择A选项。

(编辑:longyan01)